Цветовое пространство RGB
6.1. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ЦВЕТА6.1.1. Цветовое пространство
Трехмерность цвета дает основание выразить его в виде вектора в пространстве.
Выберем систему прямоугольных координат (рис. 6.1) и обозначим координатные оси символами основных цветов, например RGB. Отложим на осях числа, выражающие цветовые координаты. Положим для примера, что цвет Ц задан уравнением:
Ц = 4R + 3G + 2B. (6.1)
В соответствии с уравнением проведем вектор Ц. Его проекции на координатные оси есть цветовые составляющие 4R, 3G, 2В.
Используя координатные оси, можно найти векторы любого цвета, получаемого с помощью выбранных основных. Совокупность цветов, выраженная в данной системе основных, называется цветовым пространством системы. Каждой точке этого пространства соответствует определенный цвет, потому что любую точку можно рассматривать как конец вектора, проведенного из начала координат.
В соответствии с третьим законом Грасмана цветовые уравнения, как и обычные алгебраические, аддитивны: если складываются два цвета, то суммарный имеет цветовые координаты, равные сумме координат складываемых цветов. Следовательно, вектор суммарного цвета равен сумме векторов складываемых и может быть найден по правилу параллелограмма.
На первый взгляд векторное представление цвета может показаться излишне формальным, потому что практическое представление о нем никак не связано с одним из свойств векторной величины -- направленностью.
Вопрос о том, куда направлен цвет, например голубой, в повседневной жизни бессмыслен. Однако в цветовом пространстве вектор этого цвета имеет вполне определенное направление. Он получается аддитивным сложением синего и зеленого основных. Поэтому вектор голубого цвета лежит в координатной плоскости GB ближе к оси В, если он имеет синеватый оттенок, или к оси G, если он зеленоватого оттенка. Если голубой не насыщен, то его вектор отклонен от плоскости на тот или иной угол.
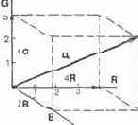
Рис. 6.1. Вектор цвета, описываемый уравнением (6.1), в пространстве RGB
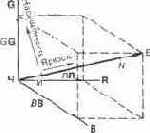
Рис. 6.2. Схема изменения характеристик цвета в зависимости от его положения в цветовом пространстве
Весьма важен вопрос об изменении насыщенности и яркости в цветовом пространстве. Поскольку ахроматические цвета имеют равные цветовые координаты, то все они находятся в цветовом пространстве на линии, равноудаленной от координатных осей. Эта линия (ЧБ на рис. 6.2) называется ахроматической осью. Чем большие численные значения имеют цветовые координаты, тем больше яркости цветов. Точке М ахроматической оси соответствует малая яркость (темно-серый цвет), а точке N — большая (светло-серый). В начале координат лежит точка Ч нулевой яркости, выражающая черный цвет. По мере продвижения по ахроматической оси от начала координат яркость возрастает. Часть оси, изображенная на рисунке, кончается точкой Б, определяющей положение белого цвета в цветовом пространстве.
Если цветовые координаты мало отличаются друг от друга, цвет, определяемый ими, находится вблизи ахроматической оси. Следовательно, насыщенность цвета в цветовом пространстве возрастает по мере удаления от ахроматической оси. Изменение насыщенности и яркости показано стрелками .
Цветовое пространство обладает некоторыми специфическими свойствами. Так, к нему неприложимо понятие расстояния, угла; в то же время можно говорить об отношениях длин и углов. Более подробно об этом будет сказано в 6.3.
6.1.2. Особые плоскости и линии цветового пространства RGB
Плоскость единичных цветов. На координатных осях RGB отложим яркости единичных значений основных цветов, выраженные в яркостных колориметрических единицах (формулы 5.1). Как известно, ВR = 1, если яркость цвета R = 680 кд-м-2; ВG = 1 при В = 3121 кд-м~2 и Вв = 1 при В = 41 кд-м-2. Следовательно, OBR, OBG, ОВВ (рис. 6.3) — единичные отрезки. Плоскость Р, проходящая через их концы, называется плоскостью единичных цветов. Любая ее точка выражает единичный цвет, т. е. такой, сумма координат которого (т. е. модуль цвета) равна единице.
Из аналитической геометрии известно уравнение плоскости в отрезках:

(6.2)
где х, у, z — текущие координаты; а, b, с — отрезки, отсекаемые плоскостью на координатных осях.
В наших обозначениях уравнение (6.2) выглядит следующим образом:
(6.2,а)
По построению BR = BG = BB = 1. Поэтому r + g + b = 1.
Следовательно, сумма цветовых координат (модуль) цвета, заданного любой точкой плоскости Р, равна единице, а значит, Р, что и требовалось доказать, есть плоскость единичных цветов, или, что то же, плоскость цвет-нос т е и. Яркость любого цвета, лежащего в ней, равна яркостной колориметрической единице, выражаемой разным числом кд-м~2
в зависимости от значения цветовых координат.
Треугольник, образованный пересечением плоскости единичных цветов с координатными плоскостями (рис. 6.3),
называется треугольником цветности или цветовым треугольником.
Плоскости равных яркостей. Цвета, лежащие на плоскости единичных цветов, имеют одинаковые яркости, выражаемые в колориметрических единицах, но разные — в кд-м~2. Определим теперь положение геометрического места точек, соответствующих постоянным значениям яркостей в кд-м^2.
Отложим на координатных осях RGB (рис. 6.4) точки S,T и U, имеющие яркости, равные 680 кд-м-2. Масштаб по ко-
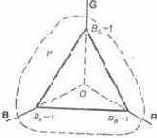
Рис. 6.3. Плоскость единичных цветов и треугольник цветности
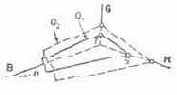
Рис. 6.4. Плоскости равных яркостей
ординатным осям выберем в яркостных колориметрических единицах BR, BG, ВB. Следовательно, для того чтобы отложить заданные точки, нужно выразить яркость 680 кд-м~2 в значениях яркостных колориметрических единиц.
680 кд-м-2 составляют одну яркостную единицу BR, 0,22 единицы BG и 17 единиц ВB.
Проведем через точки S, Т и U плоскость Q1, называемую плоскостью равных яркостей. Каждая ее точка в нашем примере выражает цвет, яркость которого равна 680 кд-м-2. Это можно доказать, приняв 680 кд-м-3 за единицу яркости и применив формулу (6.2).
Если отложить на осях координат не 680, а, например, 1360 кд-м-2 и провести через отложенные точки плоскость Q2. то она окажется параллельной Q1. Следовательно, в цветовом пространстве RGB (как и в любом цветовом пространстве) находится семейство взаимно параллельных плоскостей равной яркости. Можно вообразить себе плоскость нулевых яркостей Q0. Она параллельна Q1 и Q2 и проходит через начало координат. В ней лежат точки безъяркостных цве-
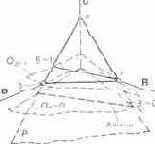
Рис. 6.5. Линии равной яркости
тов. Такие цвета, конечнб, видеть нельзя, но вообразить можно. Еще ниже расположены плоскости также воображаемых цветов, имеющих отрицательные яркости. Плоскость нулевой яркости имеет в колориметрии важное значение (см. об этом в разделе 7.3). Линии равной яркости. Линии пересечения плоскости единичных цветов с плоскостями равной яркости называются линиями равной яркости. На рис. 6.5 показаны линии В = 1 и В = 0. Последняя называется а л и х-ной. Она образована пересечением плоскостей нулевых яркостей qb=o и единичных цветов Р. На алихне лежат точки воображаемых цветов, не имеющих яркости. Представление о таких цветах используется в колориметрической системе XYZ.
6.2. ВЫРАЖЕНИЕ ЦВЕТНОСТИ
6.2.1. Свойства цветового треугольника
Для описания цветности нет необходимости прибегать к пространственным представлениям. Достаточно использовать плоскость треугольника цветности (рис. 6.3). Чтобы выразить единичный цвет численно, нужно перенести координаты с пространственных осей RGB на стороны треугольника, как это показано на рис. 6.6, а.
Из рисунка понятен метод отсчета координат от вершин треугольника. Они отсчитываются по направлению к вершине (по часовой стрелке), соответствующей данной координате. Определим координаты точки Цед (рис. 6.6, б). Чтобы найти r, нужно отсчитать эту координату по стороне gr. Для этого требуется из точки выражаемого единичного цвета Цед провести прямую, параллельную стороне bg (лежит против угла, соответствующего тому основному, координата которого отсчитывается). Так же находятся и другие координаты. Таким образом, как это
видно из рисунка, единичный цвет, выражаемый точкой Цед, описывается уравнением:
Цед = 0,3R + 0,5G + 0,2B.
Сумма координат цветности равна единице.
Пусть требуется, наоборот, по координатам цветности определить соответствующую точку треугольника. Допустим, дано уравнение
Цед=0,5R + 0,4G + 0,1В.
Для нахождения точки, цветность которой есть Ц (рис. 6.7, а), нужно из точки сторон r
= 0.5, g = 0,4 и b =

Рис. 6.6. Перенос цветовых координат (а) и пространственная интерпретация метода определения координат цветности (б) = 0,1 параллельно сторонам треугольника, противоположным вершине, выражающей основной цвет, провести прямые до их встречи в точке Ц (на рис. 6.7, а проведены пунктирными линиями).
Как видно из рисунка, третья координата лишняя. Положение точки в плоскости треугольника определяется двумя координатами. Третья не свободна, а связана со значениями двух первых. Это следует из того, что рассматриваемый треугольник — часть плоскости единичных цветов. А для характеристики цветности, которая является двухмерной величиной, достаточно двух координат. Так как сумма координат цветности равна единице, то по двум из них всегда можно найти третью. Например: r = 1 — (g + b). Аналогично для координат g и b.
Если, например, r = 0,5 и g =6,4, то третья координата q =0,1.
Цветовые свойства треугольника цветности. Выберем в треугольнике (рис. 6.7, а) точку Б с координатами r = 1/3,
g = 1/3 . В этом случае третья координата b = 1/3 . Тогда для цвета Б уравнение цветности запишется следующим образом:

Из уравнения следует, что так называемая белая точка Б (1/3, 1/3, 1/3) выражает единичный ахроматический цвет.

Рис. 6.7. Свойства треугольника цветности:
а — нахождение точки по координатам цветности; б — изменение насыщенности по биссектрисе одного из углов треугольника
Она есть след пересечения ахроматической оси цветового пространства с плоскостью единичных цветов.
Рис. 6.2 показывает, что с удалением точки от ахроматической оси насыщенность выражаемого ею цвета возрастает. Это соотношение сохраняется и для цветового треугольника. По прямой, соединяющей сторону или вершину треугольника с белой точкой, насыщенность падает от максимального ее значения в точке, принадлежащей стороне треугольника, до нулевого в белой точке. Цветовой тон на прямой остается постоянным.
Покажем это на примере изменения цветности по биссектрисе (рис. 6.7, б). Из рисунка видно, что в этом случае g = = 1—2r. Это следует из того, что заштрихованные треугольники равны между собой и, следовательно, отрезок gц1g вдвое больше отрезка rцl g. Подставив значение g в формулу b = 1 — (g + r), получим для точек биссектрисы угла g (и аналогично для других углов): b = r Следовательно, цветовые уравнения цветов, расположенных на биссектрисе угла g, имеют вид
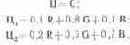
Аналогично этому насыщенность изменяется по любой прямой, проходящей через белую точку треугольника.
Пользуясь цветовым треугольником, можно складывать цвета. Поясним это, опираясь на пространственное представление. На рис. 6.8,a показан треугольник цветности, находя-

Рис. 6.8. Схема сложения цветов в треугольнике цветности:
а — пространственная интерпретация; б — соотношения на плоскости
щийся в цветовом пространстве, и векторы цветов Ц1 и Ц2, а также суммарный вектор Ц?. Плоскость параллелограмма складываемых цветов пересекает треугольник по линии
Ц1едЦ2ед
На рис. 6.8, б тот же треугольник представлен в плоскости чертежа.
Из рис. 6.8, а и б следует:
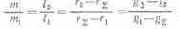
(6.3)
Если складываемые цвета Ц1 и Ц2
равны, то отрезки l1 = = Ц?едЦ1ед
и l2 = Ц2едЦ?ед
одинаковы по длине и точка суммарной цветности лежит на середине Ц1едЦ2ед. Если же яркости цветов неодинаковы, то линии отрезков Ц1едЦ2ед и Ц2сдЦ?ед обратно пропорциональны модулям складываемых цветов.
Отношение m1/m2 = l2/l1 иногда называется правилом центра
тяжести по аналогии с представлением о соотношениях между силами и плечами, принятым в механике. Белая точка. В уравнении
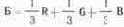
имеется в виду, что основные выражены в колориметрических единицах. Возьмем вместо этого основные в одинаковых количествах при условии, что они выражены в стандартных световых единицах. Обозначим их в знак того, что это не колориметрические единицы, символами RGB, взятыми в скобки (R)(G)(B). Тогда для получения белого цвета необходимы их количества, следующие из уравнения Б = (R) + + 4,59 (G) + 0,06 (В).
Отложим в цветовом треугольнике rgb точку Б (рис. 6.9). Модуль цвета Б в этом случае равен 5,65. Поэтому для нахождения белой точки нужно составить уравнение цветности. Деля цветовые координаты на модуль, получим r = 0,177, g= 0,813, b = 0,001.
Отложив найденную таким образом точку в треугольнике rgb (рис. 6.9), убеждаемся, что она находится не в центре, а вблизи угла g и очень близко (b = 0,001) от стороны rg. Такое положение точки белого цвета неудобно, так как точность выражения зеленых и близких к ним цветов сильно снижается, затрудняются расчеты. В этом состоит одна из причин, по которым введены колориметрические единицы яркости.
Представление основных цветов в стандартных энергетических единицах (Вт) приводит к аналогичному результату: точка Б оказывается прижатой к вершине R треугольника. В этом случае неудобно откладывать точки красных цветов и близких к ним.
Белая точка треугольника rgb выражает цветность источника Е. В треугольнике xyz есть несколько «белых» точек (см. о них в разделе 7.4).
Локус. Цветов, более насыщенных, чем спектральные, в природе не существует. Поэтому граница цветности реально наблюдаемых цветов определяется положением точек, выражающих спектральные цвета. Чтобы найти их на треугольнике, воспользуемся значениями удельных координат в системе RGB. По данным табл. 6.1, в которой приводятся значения удельных координат, найденных экспериментально, составим сначала уравнение цвета одноваттного монохроматического излучения ? = 480 нм; ц480 = 0,049R + 0,039G + 0,145 В.
Поделив каждую из координат на модуль, получим координаты цветности указанного монохроматического: r = = -0,049 : 0,135= -0,36; g = 0,039 : 0,135 = 0,29; b = 0,145-0,135 = 1,07.
Одна из координат — отрицательна. Продолжив координатные оси (рис. 6.10), можно откладывать как отрицательные значения координат цветности, так и их значения, большие единицы. Зная координаты, найдем точку, выражающую цветность излучения ? = = 480 нм, как это показано на рис. 6.10. Получим подобным же образом точки цветностей
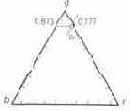
Рис. 6.9. Положение «белой» точки в случае, когда основные выражены одинаковыми числами световых единиц
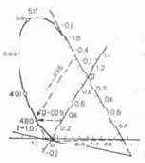
Рис. 6.10. Положение локуса относительно треугольника
цветности rgb
других монохроматических (490, 500, 510 нм и т. д.). Соединим их сплошной линией. Она называется локусом спектральных цветов или просто локусом (лат. locus — место) и является границей цветностей реально существующих цветов. Локус начинается от ? = 400 нм, доходит до ? ? ? 545 нм, а затем совпадает со стороной gr треугольника цветности.
На прямой, соединяющей любую точку локуса с белой, лежат цветности всех цветов, совпадающих по цветности со спектральными данной длины волны.
В спектре содержатся все цвета, кроме пурпурных. Чтобы получить полную совокупность максимально насыщенных цветов, локус замыкают прямой линией (на рисунке пунктир), на которой лежат единичные пурпурные максимальной насыщенности. Площадь, ограниченная локусом и замыкающей его прямой, называется полем реальных цветов.
Вне этого поля лежат воображаемые цвета, болге насыщенные, чем спектральные. На поле же находятся реальные, которые насыщены меньше лежащих на локусе.
Яркостные свойства треугольника цветности. В разделе 6.1.2 были рассмотрены линии равной яркости, образуемые пересечением плоскости единичных цветов Р с плоскостями равной яркости Qn. Яркостные свойства треугольника цветности определяются положением этих линий.
На рис. 6.11 дана изометрическая проекция треугольника, находящегося в цветовом пространстве. В таком случае координатные оси проецируются под углом 120° друг к другу. Соотношение масштабов по сторонам треугольника одинаково, и все рассуждения, относящиеся к пространственным построениям, остаются в силе и для треугольника цветности, совмещенного с плоскостью чер-
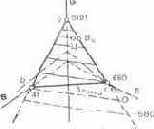
Рнс. 6.11. Распределение яркостей в треугольнике цветности rgb
тежа, как на рис. 6.7. Цифры, стоящие у вершин треугольника (рис. 6.11), показывают яркости единичных основных цветов в кд-м~2. Определив яркостный масштаб (т. е. число кд • м~2
на единицу длины по каждой из сторон), можно найти яркость цвета, выражаемого любой точкой треугольника. Найдя точки равноярких цветов и соединив их прямыми, получим линии равной яркости, которые на рис. 6.5 были представлены как следы пересечения треугольника rgb с плоскостями равных яркостей. Чтобы определить яркость произвольного цвета Ц, нужно через точку Ц провести прямую, параллельную линиям равной яркости, до пересечения с одной из сторон — bg или gr. Пусть, например, эта линия пересекает сторону gr в точке Вц. Зная яркостный масштаб сторон треугольника (кд • м-2/мм), можно по длине отрезка gBц (мм) найти яркость Вц, а следовательно, и любой точки прямой, проходящей через Ц и Вц.
6.2.2. Диаграмма rg
Общие сведения. В практике трехкоординатная система выражения цветности, рассмотренная в разделе 6.2.1, неудобна, да в ней нет и необходимости, поскольку третья координата цветности несвободна.
Поэтому эту громоздкую
6.1. Международно принятые функции сложения цветов
|
Значения ординат кривых сложения цветов в системе RGB при источнике Е |
?, нм |
Значения координат цветности спектральных излучений в системе RGB МОК (1931 г.) |
||||
|
r (?) |
g(?) |
b(?) |
r(?) |
g(?) |
b(?) |
|
|
0,00003 |
—0,00001 |
0,00117 |
380 |
0,0272 |
—0,0115 |
0,9843 |
|
0,00005 |
—0,00002 |
0,00189 |
385 |
0,0268 |
—0,0114 |
0,9846 |
|
0,00010 |
—0,00004 |
0,00359 |
390 |
0,0263 |
—0,0114 |
0,9851 |
|
0,00017 |
—0,00007 |
0,00647 |
395 |
0,0256 |
— 0.01L3 |
0,9857 |
|
0,00030 |
-0,00014 |
0,01214 |
400 |
0,0247 |
—0,0112 |
0,9865 |
|
0,00047 |
—0,00022 |
0,01969 |
405 |
0,0237 |
—0,0111 |
0,9874 |
|
0,00084 |
—0,00041 |
0,03707 |
410 |
0,0225 |
—0,0109 |
0,9884 |
|
0,00139 |
—0,00070 |
0,06637 |
415 |
0,0207 |
—0,0104 |
0,9897 |
|
0,00211 |
—0,00110 |
0,11541 |
420 |
0,0181 |
—0,0094 |
0,9913 |
|
0,00266 |
—0,00143 |
0,18575 |
425 |
0,0142 |
— 0..0076 |
0,9934 |
|
0,00218 |
— 0,001 19 |
0,24769 |
430 |
0,00088 |
—0,0048 |
0,9960 |
|
0,00036 |
—0,00021 |
0,29012 |
435 |
0,0012 |
—0,0007 |
0,9995 |
|
—0,00261 |
0,00149 |
0,31228 |
440 |
—0,0084 |
0,0048 |
1 ,0036 |
|
—0,00673 |
0,00379 |
0,31860 |
445 |
—0,0213 |
0,0120 |
,0093 |
|
—0,01213 |
0,00678 |
0,31670 |
450 |
—0,0390 |
0,0218 |
,0172 |
|
—0,01874 |
0,01046 |
0,31166 |
455 |
-0,0618 |
0,0345 |
,0273 |
|
—0,02608 |
0,01485 |
0,29821 |
460 |
—0,0909 |
0,0517 |
,0392 |
|
—0,03324 |
0,01977 |
0,27295 |
465 |
—0,1281 |
0,0762 |
,0519 |
|
—0,03933 |
0,02538 |
0,22991 |
470 |
—0,t821 |
0,1175 |
,0646 |
|
—0,04471 |
0,03183 |
0,18592 |
475 |
—0,2584 |
0,1840 |
,0744 |
|
—•0,04939 |
0,03914 |
0,14494 |
480 |
—0,3667 |
0,2906 |
,0761 |
|
—0,05364 |
0,04713 |
0,10968 |
485 |
—0,5200 |
0,4568 |
,0632 |
|
—0,05814 |
0,05689 |
0,08257 |
490 |
—0,7150 |
0,6996 |
,0154 |
|
—0,06414 |
0,06948 |
0,06246 |
495 |
—0,9459 |
,0247 |
0,9212 |
|
—0,07173 |
0,08536 |
0,04776 |
500 |
—1 , 1685 |
,3905 |
0,7780 |
|
—0,08120 |
0,10593 |
0,03688 |
505 |
—1,3182 |
,7195 |
0,5987 |
|
—0,08901 |
0,12860 |
0,02698 |
510 |
-1,3371 |
,9318 |
0,4053 |
|
—0,09356 |
0,15262 |
0,01842 |
515 |
— 1,2076 |
,9699 |
0,2377 |
|
—0,09264 |
0,17468 |
0,01221 |
520 |
—0,9830 |
,8534 |
0,1296 |
|
—0,08473 |
0,19113 |
0,00830 |
525 |
—0,7386 |
1,6662 |
0,0724 |
|
—0,07101 |
0,20317 |
0,00549 |
530 |
—0,5159 |
1,4761 |
0,0398 |
|
—0,05316 |
0,21083 |
0,00320 |
535 |
—0,3304 |
1,3105 |
0,0199 |
|
—0,03152 |
0,21466 |
0,00146 |
540 |
—0,1707 |
1 , 1628 |
0,0079 |
|
—0,00613 |
0,21487 |
0,00023 |
545 |
—0,0293 |
1,0282 |
0,0011 |
|
0,02279 |
0,21178 |
—0,00058 |
550 |
0,0974 |
0,9051 |
—0,0025 |
|
0,05514 |
0,20588 |
—0,00105 |
555 |
0,2121 |
0,7919 |
—0,0040 |
|
0,09060 |
0,19702 |
—0,00130 |
560 |
0,3164 |
0,6881 |
—0,0045 |
|
0,12840 |
0,18522 |
—0,00138 |
565 |
0,4112 |
0,5932 |
—0,0044 |
|
0,16768 |
0,17087 |
—0,00135 |
570 |
0,4973 |
0,5067 |
—0,0040 |
|
0,20715 |
0,15429 |
—0,00123 |
. 575 |
0,5751 |
0,4283 |
—0,0034 |
|
0,24526 |
0,13610 |
—0,00108 |
580 |
0,6449 |
0,3579 |
—0,0028 |
|
0,27989 |
0,11686 |
—0,00093 |
585 |
0,7071 |
0,2952 |
—0,0023 |
|
0,30928 |
0,09754 |
—0,00079 |
590 |
0,7617 |
0,2402 |
—0,0019 |
|
0,33184 |
0,07909 |
—0,00063 |
595 |
0,8087 |
0,1928 |
—0,0015 |
|
0,34429 |
0,06246 |
—0,00049 |
600 |
0,8475 |
0,1537 |
—0.0012 |
|
0,34756 |
0,04776 |
— о;оооз8 |
605 |
0,8800 |
0,1209 |
—0,0009 |
|
0,33971 |
0,03557 |
—0,00030 |
610 |
0,9059 |
0,0949 |
—0,0008 |
Продолжение табл. 6.1
|
Значения ординат кривых сложения цветов в системе RGB при источнике Е |
?, нм |
Значения координат цветности спектральных излучений в системе RGB МОК (1931 г.) |
||||
|
r(?) |
g(?) | b(?) |
r(?) |
g(?) |
b(?) |
||
|
0,32265 |
0,02583 |
—0,00022 |
615 |
0,9265 |
0,0741 |
—0,0006 |
|
0,29708 |
0,01828 |
—0,00015 |
620 |
0,9425 |
0,0580 |
—0,0005 |
|
0,26348 |
0,01253 |
—0,00011 |
625 |
0,9550 |
0,0454 |
—0,0004 |
|
0,22677 |
0,0983-3- |
—0,00008 |
630 |
0,9649 |
0,0354 |
—0,0003 |
|
0,19233 |
0,00537 |
—0,00005 |
635 |
0,9730 |
0,0272 |
—0,0002 |
|
0,15968, |
0,00334 |
—0,00003 |
640 |
0,9797 |
0,0205 |
—0,0002 |
|
0,12905 |
0,00199 |
—0,00002 |
645 |
0,9850 |
0,0152 |
—0,0002 |
|
0,10167 |
0,00116 |
—0,00001 |
650 |
0,9888 |
0,0113 |
—0,0001 |
|
0,07857 |
0,00066 |
—0,00001 |
655 |
0,9918 |
0,0083 |
—0,0001 |
|
0,0о932 |
0,00037 |
0,00000 |
660 |
0,9940 |
0,0061 |
—о.ооо г |
|
0,04366 |
0,00021 |
|
665 |
0,9954 |
0,0047 |
—0,0001 |
|
0,03149 |
0,00011 |
|
670 |
0,9966 |
0,0035 |
—0,0001 |
|
0,02294 |
0,00006 |
|
675 |
0,9975 |
0,0025 |
0,0000 |
|
0,01687 |
0,00003 |
|
-680 |
0,9984 |
0,0016 |
|
|
0,01187 |
0,00001 |
|
685 |
0,9991 |
0,0009 |
|
|
0,00819 |
0,00000 |
|
690 |
0,9996 |
0,0004 |
|
|
0,00572 |
|
|
695 |
0,9999 |
0,0001 |
|
|
0,00410 |
|
|
700 |
1 , 0000 |
0,0000 |
|
|
0,00291 |
|
|
705 |
1,0000 |
|
|
|
0,00210 |
|
|
710 |
1,0000 |
|
|
|
0,00148 |
|
|
715 |
1,0000 |
|
|
|
0,00105 |
|
|
720 |
1,0000 |
|
|
|
0,00074 |
|
|
725 |
1,0000 |
|
|
|
0,00052 |
|
|
730 |
1,0000 |
|
|
|
0,00036 |
|
|
735 |
1,0000 |
|
|
|
0,00025 |
|
|
740 |
1,0000 |
|
|
|
0,00017 |
|
|
745 |
1,0000 |
|
|
|
0,00012 |
|
|
750 |
1,0000 |
|
|
|
0,00008 |
|
9> |
755 |
1 ,0000 |
|
|
|
0,00006 |
|
|
760 |
1,0000 |
|
|
|
0,00004 |
|
|
765 |
1,0000 |
|
|
|
0,00003 |
|
г> |
770 |
1,0000 |
|
|
|
0,00001 |
|
Чэ |
775 |
1,0000 |
|
|
|
0,00000 |
|
|
780 |
1,0000 |
|
|
Яркостные коэффициенты LR : LG : LB= 1 : 4,5907 : 0,0601
систему заменяют обычной прямоугольной. Представим себе (рис. 6.12) треугольник цветности rgb с локусом и прямой пурпурных цветов (поле реальных цветов), находящих-сях в пространстве RGB. Локус показан на рисунке штриховыми линиями, потому что находится в октанте G — RB. Спроецируем-изображенную на рисунке фигуру на координатную плоскость GR—R. Тогда проекция вершины b -точка b' совпадает с точкой О — началом координат. Ось

Рис. 6.12. Проекционное преобразование треугольника rgb с локусом
Og в этом случае — ось ординат декартовой системы, а ось Or — ось абсцисс.
Проекционно преобразованное поле реальных цветов, включая треугольник rgb, показано на рис. 6.12 (заштриховано). На рис. 6.13 оно совмещено с плоскостью чертежа. Колориметрические свойства треугольника, полученного таким путем, не отличаются от свойств исходного равностороннего.
1. Значения цветовых координат цветов не изменяются от проекционного преобразования.
2. Насыщенность цветов по-прежнему возрастает от белой точки к локусу.
3. На прямой, проходящей через целую точку, лежат, как и в равностороннем треугольнике, цветности цветов постоянного цветового тона.
4. На прямой, соединяющей точки двух цветностей, находятся точки их суммарных цветов; расстояния точки суммарного цвета дс точек складываемых цветов обратны модулям последних.
5. Белая точка имеет, как и раньше, координаты Б (1/3; 1/3).
6. Локус остается границей спектральных цветов.
7. Алихна остается линией нулевых яркостей.
Подобные проекционные преобразования в колориметрии применяются часто. Они упрощают определения и расчёты. При них сохраняются метрические свойства не только треугольника, но и цветового пространства. Широко используется как ортогональное проецирование, так и более сложные, как в рассмотренном примере, случаи проекционных преобразований.
Сетка прямоугольных координат с нанесенным на нее локусом, замкнутым прямой пурпурных цветов, называется диаграммой цветности или цветовым графиком.
Выражение цветового тона через доминирующую длину волны и насыщенности через колориметрическую чистоту. Цветовой график можно использовать для определения до минирующей длины волны и колориметрической чистоты (см. с. 34).
Цветовой тон. Возьмем на диаграмме цветности произвольную точку Ц (рис. 6.13). Пусть она имеет, например, координаты Ц (0,2; 0,6). Соединим ее с белой точкой и продолжим линию вверх до пересечения с локусом. На проведенной таким образом прямой изменяется только насыщенность, и точка пересечения Ц?=550
соответствует длине волны излучения, имеющего тот же цветовой тон, что и цвет Ц, т. е. доминирующей длине волны.
Так как пурпурных в спектре, а следовательно, на локусе нет, то для них рассматриваемая характеристика находится следующим образом. Возьмем вблизи линии пурпурных цвет П. Найдем цвет, тождественный ему по тону, но максимальной насыщенности. Для этого соединим точку П с белой точкой и продолжим прямую пересечения с линией пурпурных. Точка пересечения П выражает тот же цветовой тон, что и точка П. Продолжим теперь прямую ПБ в сторону локуса. Точка пересечения указывает длину волны ? = 500 нм. Это — цвет, дополнительный к П. Его длиной волны со знаком «штрих» обозначается точка П на линии пурпурных. В нашем примере доминирующая длина волны равна 500' нм.
Колориметрическая чистота цвета. Зная положение цвета Ц на диаграмме цветности (рис. 6.13), можно найти его колориметрическую чистоту р по формуле
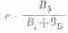
Заменив В? + ВБ
= В, получим р = В? : В.
Для расчета колориметрической чистоты по данным, которые можно прочитать на диаграмме, следует яркости В?
и В заменить их значениями в соответствии с формулой 5.5:

(6.4)
Преобразуем отношение m?/m так, чтобы к нему можно было приложить правило сложения цветов по формуле (6.3):
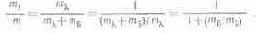
Из (6.3) следует:

Взяв отношение модулей mБ/m? вместо отношения отрезков
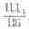
проведем обратное преобразование:

Из (6.4) будем иметь
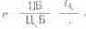
(6.5)
где первый сомножитель — отношение расстояния от точки определяемого цвета до белой к расстоянию от белой точки до локуса.
Различают два близких понятия — условная чистота цвета ру и собственно колориметрическая чистота цвета р (иногда ее обозначают рк). При определении ру яркостные коэффициенты выражают как 1/680 долю колориметрической единицы основных. В этом смысле яркостные коэффициенты равны между собой. Тогда
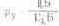
При определении р отношение L?/L выражается в световых единицах яркости, и, следовательно,

Для практических расчетов отношение расстоянии ЦБ/Ц?Б
заменяют пропорциональным ему отношением разностей координат, которое легко прочитать по координатным осям диаграммы. Например, для цвета Ц (рис. 6.14):
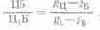
для цвета Ц1:
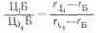
для цвета Ц2 (точка Ц?2
лежит на линии пурпурных цветов, совпадая с точкой П).
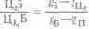
Для цветов, расположенных за локусом, чистота больше единицы. Так, для Ц3:
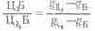
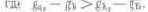

Рис. 6.13. К выражению колориметрической чистоты цвета на диаграмме rg и выводу уравнения алихны
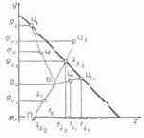
Рис. 6.14. Схема определения колориметрической чистоты цвета
В колориметрической практике применяют диаграммы, на которых точки цветов одинаковой чистоты соединены линиями. Таким образом, значение этой величины можно прочитать по диаграмме.
Положение линии алихны. Яркость единичного цвета в соответствии с (5.4) равна Вц
= 680 (rLR + gLG + bLB).
Приравняв это уравнение нулю и выразив яркостные коэффициенты через соответствующие им яркости, получим для алихны:
680(r + 4,59g+0,06b) = 0. (6.6)
Уравнение выражает положение алихны в пространстве. Чтобы описать ее положение на плоскости, необходимо заменить b значением 1 — (r + g).
Подставив это значение координаты в уравнение (6.6), находим после преобразования
g = — 0,208 r— 0,013. (6.7)
Угловому коэффициенту уравнения (6.7) соответствует угол ? = 168° относительно оси абсцисс. Проводя под этим углом прямую, отсекающую от оси ординат отрезок g =
—0,013, получим алихну (рис. 6.13), обозначена тонкой линией.
6.3. АФФИННЫЕ СВОЙСТВА ЦВЕТОВОГО ПРОСТРАНСТВА
В соответствии с первым законом Грасмана основные цвета должны быть линейно независимыми.
Это значит, что они могут быть представлены любыми тремя векторами, лишь бы эти векторы не лежали в одной плоскости. Таким образом, декартова система координат, на которой был основан изложенный выше материал о цветовом пространстве, — лишь частный случай представления векторного пространства цветов. Для выражения совокупности цветов иногда применяют систему косоугольных координат как более общую, чем прямоугольная.
Изменение углов между координатными осями приводит к деформации цветового пространства. Например, при уменьшении указанных углов точки цветов (или, что то же, концы векторов) смещаются к ахроматической оси. Естественно, что совокупность цветов при этом остается прежней, происходит лишь их перемещение — сжатие цветового пространства. При увеличении углов, наоборот, цветовое пространство расширяется. Однако все его метрологические свойства (главные из них отмечены в разделе 6.2) при указанных деформациях сохраняются. Сохраняются они и при изменении длин векторов основных цветов, хотя это действие, как и упомянутые, приводит к перемещению цветов в пространстве. Во всех этих случаях деформации пространства изменяются также форма и положение цветового треугольника.
Таким образом, существуют геометрические преобразования цветового пространства, при которых его метрологические свойства остаются прежними. Это главным образом — аффинные преобразования (от лат. affinis — родственный).
Пусть х и у.— декартовы координаты некоторой точки на плоскости. Аффинное преобразование состоит в том, что х и у превращаются в новые координаты х1 и y1 связанные с исходными соотношениями:
х1 = ах+bу+р;
y1= cx+dy+q, (6.8)
где ad — bc ? 0.
Изучением аффинных преобразований занимается раздел математики — аффинная геометрия. Здесь будет рассмотрен только частный случай, чтобы дать представления, не-

Рис. 6.15. Примеры аффинного преобразования: а — схема преобразования; 6 — результат преобразования обходимые для понимания некоторых свойств цветового пространства.
Примером аффинных преобразований служат преобразования подобия, а также получаемые равно мерным сжатием или расширением изображения. Случай такого преобразования был показан на рис. 6.12: проецируемая плоскость и плоскость проекции непараллельны. Представим его более наглядно. На рис. 6.15, а показаны проецируемая плоскость Р, в которой находится ряд фигур, и плоскость проекции Р'. Изображения фигур в результате проецирования сужаются в направлении, перпендикулярном линии пересечения плоскостей, т. е. происходит их аффинное преобразование. Его следствия представлены на рис. 6.15, б.
Свойства фигур, которые сохраняются при рассматриваемом преобразовании.
1. Параллельность прямых: пары отрезков 1 и 2 остаются параллельными и в проекционной копии.
2. Отношения углов: меньший угол в примере 4 и в проекции остается вдвое меньшим, чем больший.
3. Плоскостность фигур.
4. Отношения параллельных отрезков: короткий отрезок и в копии составляет 2/3 длинного, независимого от их расположения в оригинале (примеры / и 2).
Представим себе, что плоскость Р, показанная на рис. 6.15, а, есть одна из координатных плоскостей прямоугольной системы координат, ограничивающих цветовое пространство, а Р' --косоугольной. От замены плоскости Р на Р' аффинные свойства цветового пространства, определяющие его метрологические особенности (см. ниже), не нарушаются. Это делает понятной упомянутую выше произвольность выбора угла между координатными осями основных цветов.
Свойства фигур и линий, которые не сохраняются при аффинных преобразованиях, называются н е а ф ф и н-н ы м и (рис. 6.15).
1. Расстояния между параллельными прямыми (примеры / и 2) в общем случае не сохраняются.
2. При аффинности отношения углов сами углы неаф-финны; как видно из примеров 3, 4 и 5, они могут при аффинных преобразованиях измениться.
3. Форма фигуры в результате описываемого преобразования может измениться: равносторонний треугольник rgb (рис. 6.12) превращается в прямоугольный, соотношения осей эллипсов (пример 7) изменяются, окружность может перейти в эллипс (пример 6), а эллипс — в окружность (пример 8).
4. Отношения длин непараллельных отрезков также неаффинны: отрезки из примера / сохраняют длину, а отрезки 2 становятся более короткими, и отношения длин указанных пар в оригинале и копии различны.
Рассмотрим теперь несколько примеров, иллюстрирующих метрологический смысл аффинных и неаффинных свойств цветового пространства.
Сравнение длин в цветовом пространстве, обладающем аффинными свойствами, имеет смысл только для одного направления (см. случай неаффинности 4 и примеры 1 и 2 на рис. 6.15, а). Сравнивать длины векторов цветов, направленных в разные стороны, строго говоря, нельзя: их отношение неаффинно. Из этого вытекает невозможность непосредственного сравнения яркостей качественно различных цветов (т. е. длин векторов, направленных в разные стороны). Для решения такой задачи, как говорилось в 2.2.1, существуют искусственные приемы.
Отмеченная выше неаффинность углов и аффинность их отношений имеет следующее значение. Насыщенность цветов разного цветового тона определяется углами их векторов с ахроматической осью, возрастая с увеличением этого угла. Но так как углы неаффинны, то насыщенности цветов разного цветового тона непосредственно несравнимы (существуют, однако, как мы видели, обходные пути). В то же время насыщенность цветов одного и того же цветового тона сравнивать можно. Это объясняется тем, что векторы цветов и ахроматическая ось в этом случае лежат в одной плоскости. Угол, составляемый вектором меньшей насыщенности с указанной осью, есть доля угла, образуемого с ней вектором цвета большой насыщенности. Отношения же углов аффинны.
В связи с рассмотренным свойством цветового пространства становится понятным определение цвета по ГОСТ 13088—67: «Цвет есть аффинная векторная величина трех измерений, выражающая свойство, общее всем спектральным составам излучения, визуально неразличимым в колориметрических условиях наблюдения».
Определение цвета как аффинной векторной величины означает, что те его свойства, которые аффинны, сохраняются при преобразованиях, удовлетворяющих уравнениям (6.8).
